GPS Navigation
Grundlagen der Positionsbestimmung
Die mathematischen Grundlagen der Positionsbestimmung auf der Erde mittels GPS Satelliten findet man in epischer Breite in
zahlreichen Veröffentlichungen, in der Wikipedia und auf Seiten der NASA, die mit dem Navstar Programm Anfang der 80er Jahre die
Entwicklung einleitete. Gedacht war das System zur Steuerung von Kampfschiffen und der Preis von etwa 1 Mio. DM für einen
Empfänger schränkte den Nutzerkreis auf interessierte Stellen und auf das Militär ein. Damals machten die seltenen und wertvollen Geräte lange
Reisen, so z.B. vom Institut für Geodäsie der Universität Bonn in die Antarktis und eine einzige Koordinatenbestimmung dauerte vielleicht einen Tag und
mehr. Damals waren nämlich nicht nur die Empfänger selten, sondern auch die Satelliten, sodass die erforderliche Anzahl von vier Satelliten
nicht permanent über dem Horizont sichtbar war. Damals war die Rechenleistung eines Hochschulrechenzentrums geringer als das, was
heute in jedem Wohnzimmer steht. Und da die Amerikaner aus Angst vor der hochgenauen Bestimmung des Erschwerefeldes die gesendeten Bahndaten
der Satelliten verfälschten, durften nur sicherheitsdienstlich überprüfte Mitarbeiter die tatsächlichen Bahndaten nachträglich auswerten, was letztlich erst auf geodätisch brauchbare Ergebnisse führte.
 *
*
Mathematik zu erklären ohne Mathematik zu benutzen ist eine Kunst, die nur wenige Redakteure einer Wissenschaftsredaktion beherrschen - und
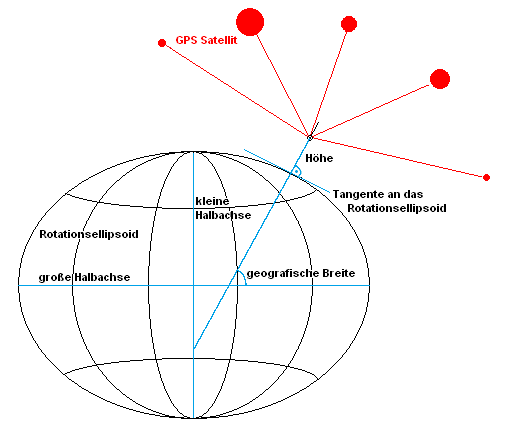
mit denen will ich nicht konkurrieren. Trotzdem soll hier das prinzipielle Modell gezeigt werden, das mit der Tangente an die Erde zugleich
die für Karten übliche Ebene der Projektion darstellt. Die Höhe repräsentiert den Abstand des Beobachters vom Ellipsoid, gemessen entlang der Flächennormalen.
 *
**
GPS Satelliten fliegen auf polnahen Bahnen um die Erde und senden dabei Signale aus, die Informationen über die aktuelle
Position enthalten und über den Zeitpunkt der Ausstrahlung. Dieser Zeitpunkt ist entscheidend für die Berechnung der Signallaufzeit, die aus der
Differenz von Sende- und Empfangszeitpunkt berechnet wird. Aus der Position der Satelliten und der Strecke zum Beobachter, die sich als
Produkt aus Laufzeit und Lichtgeschwindigkeit ergibt, lassen sich theoretisch die drei unbekannten Koordinaten des Beobachters im Raum
berechnen. Leider ist der Empfangszeitpunkt wegen der großen Geschwindigkeit des Lichts nicht mit hinreichender Genauigkeit zu
reproduzieren; dazu müsste man Atomuhren durch die Gegend schleppen.
Deshalb wird der Empfangszeitpunkt als vierte Unbekannte in die Gleichungen eingeführt, weshalb eine vierte Beobachtung (und damit
ein vierter Satellit) zur Lösung des Gleichungssystems erforderlich ist. Das Bild zeigt einen fünften Satelliten, womit das
Gleichungssystem überbestimmt ist. Statt dieses nach gängigen Ausgleichungsverfahren zu
lösen und die gewonnene Genauigkeit durch einen erheblichen zusätzlichen Rechenaufwand zu erkaufen, ermittelt der GPS
Empfänger zumeist den geometrisch günstigsten Schnitt aus den möglichen Kombinationen. Die Berechnung der Schnittgenauigkeit ist zudem nur
periodisch erforderlich, da sich die Satellitenkonstellation mit der Zeit moderat ändert. Heute fliegen ca. 36 Satelliten etwa 20000 km über der Erde,
wodurch bei großer Horizontfreiheit etwa zehn Satelliten zugleich sichtbar sind. Die Zahl variiert etwas, weil nicht immer alle gleichzeitig in Betrieb sind.*
Sehr viel weiter gehen die Ausführungen gab es früher auf kowoma, noch vor kurzem eine wirklich lesenswerte Seite des Netzes! Mittlerweile
wurde der Betrieb eingestellt.